Existen muchos métodos que nos permiten aproximarnos al mágico número \(\pi\). Con un poco de astucia podemos, pensando un poco, imaginar un método para su aproximación. Lo difícil es que seamos capaces de inventar algo eficiente. Hace algún tiempo comentaba este tema con un amigo. Hablábamos de la Aguja de Buffón, un método que yo acababa de conocer y que me dejó pasmado, pues es tremendamente ocurrente y no demasiado complejo. Éste método nos dice que, si tenemos una aguja de longitud \(l\) y la dejamos caer de forma aleatoria sobre un plano dividido en lineas paralelas entre sí una distancia \(D \leq l\), la probabilidad de que la aguja corte a alguna linea es de \(\frac{2}{\pi}\) . De ahí, y suponiendo \(N\) agujas totales y \(A\) agujas que cortan una linea, tenemos que \({\pi} = \frac{2N}{A}\). Cuantas más agujas tiremos, mejor aproximación obtendremos de \(\pi\). La demostración en el enlace de antes.

Éste método es bastante lento, pues ganamos unos pocos decimales por cada cientos de iteraciones. Pero lo curioso del asunto no es la eficiencia, sino la ocurrencia del método. Si de verdad queremos una buena aproximación deberíamos interesarnos por las Series de Ramanujan (nada recomendable sin un buen nivel de matemáticas), que convergen a con velocidades de vértigo. Especialmente la descubierta por los hermanos Chudnovsky en 1987, que ofrece ni más ni menos que 15 cifras decimales de \(\pi\) por término:

\[\frac{1}{\pi} = 12 \sum^\infty_{k=0} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 640320^{3k + 3/2}}\!\]

Existen otros métodos para las aproximaciones de \(\pi\). Si queréis mas información, echad un vistazo al Algoritmo de Borwein, de orden de convergencia 4 (en cada iteración se cuadruplica el número de decimales) y a sus derivaciones, el Algoritmo de Gauss-Legendre/Brent-Salamin con convergencia de segundo orden, la Fórmula de Bailey-Borwein-Plouffe que permite calcular el n-ésimo dígito de sin necesidad de calcular los anteriores (¡realmente interesante!), la Fórmula de Leibniz, el Algoritmo de Liu Hui que es bastante gráfico (aunque no tanto como el que enseñaré luego), las fórmulas de tipo Machin, que es el método que se usó para batir el record de cómputo de decimales de \(\pi\), la solución de Euler al Problema de Basilea o el Producto de Wallis del que hablaré otro día.

El método de la diana

Imaginemos un círculo inscrito en un cuadrado de lado \(2u\) como el siguiente: cuadrado_2u.png Con lo listo que somos, seguro que nos damos cuenta que el radio del círculo inscrito es de \(1u\). También sabemos que el área de cuadrado es \(A_{cuad} = 4u^2\) y que \(A_{circ} = r^2 = \pi\).

Imaginemos ahora que esa figura es una diana con la que vamos a jugar a los dardos. ¿Cuál es la probabilidad de que nuestro dardo clave en la diana (círculo) y no en el marco (cuadrado)?

La probabilidad de que el dardo se clave en la diana viene dada por la relación entre el área del círculo y el cuadrado, es decir, \(\frac{\pi}{4}\). Podemos expresarla también como la relación \(\frac{dardos_{diana}}{dardos_{total}}\). Si igualamos: \(\frac{dardos_{diana}}{dardos_{total}}=\frac{\pi}{4}\), y despejando obtenemos \(\pi =4 \times \frac{dardos_{diana}}{dardos_{total}}\). Si alguna vez nos aburrimos y decidimos tirarnos una semana tirando dardos con los ojos vendados (para que los disparos sean aleatorios), veremos como existe una relación entre el número de dardos que lanzamos y los que dan en la diana que tiende a \(\pi\). Sabido esto, es sencillo implementarlo en el lenguaje de programación que más nos guste, aunque si se prefiere, se puede optar por la opción de estar una semana tirando dardos con los ojos vendados. Yo he preferido hacer uso de python+pythong (para la creación de gráficos):

def pi_diana(disparos):
    create_rectangle(0, 0, 1000, 1000, "blue")
    create_circle(500, 500, 500, "red")

    dentro = 0

    for i in range(disparos):
        x = random() * 1000
        y = random() * 1000

        if sqrt(pow(500 - x, 2) + pow(500 - y, 2)) < 500:
            create_point(x, y, "green")
            dentro += 1
        else:
            create_point(x, y, "red")

    return float(4 * dentro / float(disparos))

El resultado es el siguiente: pi-diana-resultados.png

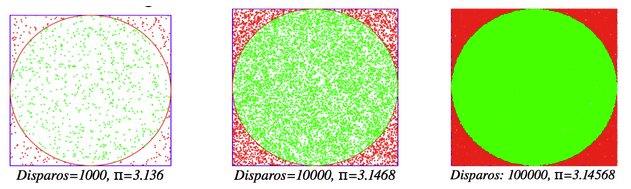
Como se puede observar, el resultado no es muy bueno, pues se necesitan muchas iteraciones para conseguir unas mínimas cifras significativas, pero sí que es curioso el comprobar cómo puede calcularse un número tan mágico como \(\pi\) de una forma tan peculiar.

¿Quién nos iba a decir que π está presente cuando jugamos a los dardos?